Maintenant que la Coupe du monde est terminée, on voit fleurir ici et là des critiques contre les modèles utilisés pour en prédire le résultat, au prétexte qu’ils se seraient « trompés ». Mais peut-on prédire le vainqueur d’une compétition sportive ?
Les humains ont du mal à raisonner en probabilités, et les commentaires sur les modèles prédictifs en donnent une belle illustration. Les critiques sont en effet nombreuses contre les modèles utilisés pendant la Coupe du monde, comme par exemple ce tweet du journaliste scientifique Pierre Barthélémy qui reprend un article de Bloomberg :
https://twitter.com/PasseurSciences/status/1018816416588365825
La principale cible de ces critiques (pour ne pas dire moqueries) est un modèle de la banque d’affaires Goldman Sachs. Je suspecte que ces moqueries soient en partie dues au fait que le modèle vienne d’une banque d’affaire[1], mais à la rigueur peu importe.
De manière plus fondamentale, ces modèles de prédiction posent une question plus profonde qu’il n’y paraît : pour faire des prédictions qui ont un sens, il faut disposer d’un bon modèle prédictif. Mais comment s’assurer que l’on a effectivement un bon modèle prédictif entre les mains ?
De manière générale, ces modèles sont probabilistes : ils estiment la probabilité, pour un match donné, que l’une ou l’autre des deux équipes l’emporte. Par exemple, des doctorants en économie de l’Université de Rennes ont estimé que l’Angleterre avait 66% de l’emporter face à la Croatie en demi-finale – la Croatie ayant donc 34% de chances de l’emporter face à l’Angleterre en demi-finale.
Toutefois, à la fin c’est bien la Croatie qui l’a emporté, plutôt que l’Angleterre. Peut-on en conclure que le modèle de prédiction était faux, ou s’est trompé ? Probablement pas.
La première difficulté à laquelle il faut faire très attention est la représentation des probabilités : 34% de chances de l’emporter pour la Croatie, c’est certes moins que l’Angleterre, mais ça reste élevé. Le meilleur moyen de s’en rendre compte est de représenter 1000 cases, et d’en colorer autant en rouge que l’équipe a de chances de l’emporter.
Si l’on commence par l’Angleterre, on se rend compte de son statut de « favori » sur ce match, avec 666 cases colorées :

Voici le même graphique, mais pour la Croatie et ses 334 cases colorées :

À la vue du second graphique, on se rend bien compte que si l’on tirait une case au hasard, il est loin d’être impossible d’en tirer une rouge. En d’autres termes, 34% de chances de l’emporter pour la Croatie, c’est loin d’être négligeable !
Plutôt qu’interpréter ces modèles prédictifs sur un mode « X va l’emporter face à Y », il me semble qu’il serait plus avisés de les interpréter comme une représentation quantitative du rapport de force entre les deux équipes qui vont s’affronter. Avec l’idée que plus l’écart entre les deux probabilités de gagner est élevée, plus la différence de niveau entre les deux équipes est susceptible de jouer un rôle dans le résultat du match[2]. C’est un outil que je vois en plus du commentaire sportif classique, pas à la place – et certainement pas comme un outil pour jouer aux devins du dimanche.
Un exemple de (grossière) erreur d’interprétation de ces modèles est à chercher dans ce titre de Libération, daté du 13 juin :
Le modèle décrit dans cet article provient d’une équipe de chercheurs autrichiens, qui ont produit ce graphique des probabilités des équipes de remporter la Coupe du monde avant qu’elle ne commence[3] :
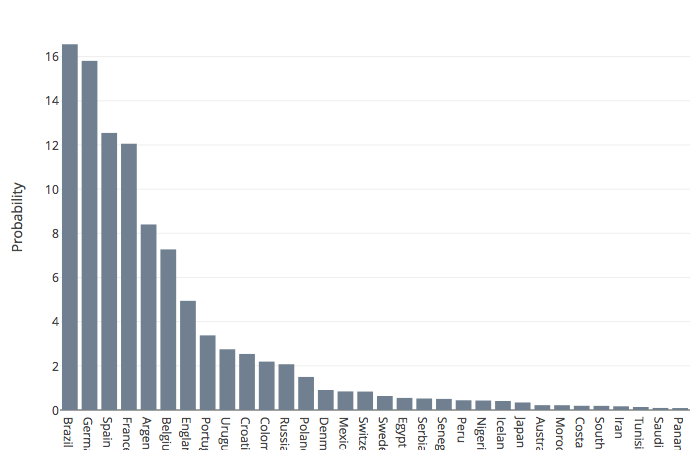
Pour commencer, ce graphique ne permet aucunement de prédire l’affiche de la finale. Il dit que le Brésil était favori, suivi par l’Allemagne. Mais il ne dit pas du tout que la finale opposera ces deux équipes.
Surtout, « les stats sont formelles » est une totale sur-interprétation : quatre équipes avaient environ 15% de chances de l’emporter, le Brésil, l’Allemagne, l’Espagne et la France. Si l’on ajoute la marge d’erreur, dire que ces prédictions sont « formelles » n’a aucun sens. À titre de comparaison, en science économique on considère une hypothèse comme « vraie » si la probabilité qu’elle le soit est au moins de 95%, voire de 99% – en physique, le seuil est même à 99.99998%… Et encore, puisqu’on fait de la science, on interprète ces résultats en ayant en tête le fameux « jusqu’à preuve du contraire ». Alors parler de certitudes pour une probabilité de 15%, vous comprendrez que ça me fait grincer des dents…
Outre ces difficultés à correctement interpréter les résultats des modèles prédictifs, le deuxième problème posé par ces modèles est de nature épistémologique : à partir de quel moment peut-on dire que ces modèles sont « faux » ? Ou, en d’autres termes, comment peut-on les valider ?
Si l’on reprend l’exemple du match Angleterre-Croatie, la Croatie l’ayant emporté alors que la probabilité de victoire de l’Angleterre était plus élevée, on serait tenté d’en conclure que le modèle s’est « trompé ». Sauf qu’on l’a vu plus haut : 34% de chances de l’emporter, c’est en réalité substantiel[4]. Et même si la probabilité calculée avait été de 1%, ou même de 0,1%, que l’équipe pour laquelle cette faible probabilité est calculée l’emporte ne permet pas d’invalider rigoureusement le modèle. Parce que c’est un modèle probabiliste. Et un « contre-exemple » ne permet pas de le réfuter. Prenons un petit exemple pour comprendre pourquoi.
Imaginons une équipe de sociologues qui calcule qu’un enfant dont les parents sont ouvriers a 80% de chances d’être lui-même ouvrier. Est-ce qu’un enfant dont les parents sont ouvriers, mais qui termine ingénieur par exemple, ou chercheur, contredit ce modèle ? Non, car ce modèle laisse ouvert la possibilité que 20% des enfants dont les parents sont ouvriers ne deviennent pas eux-mêmes ouvriers.
Pour valider, ou invalider, un modèle probabiliste, il faut le confronter à un grand nombre d’observations. Au moins 1.000, davantage si l’on veut que la marge d’erreur soit la plus réduite possible ou si le modèle est complexe.
Pour le modèle des sociologues, il faut le tester non pas en regardant le destin d’un seul enfant, mais le destin de 1.000, 10.000 ou 100.000 enfants. Si sur 100.000 enfants dont les parents sont ouvriers, environ 80.000 finissent eux-aussi ouvriers, alors le modèle est validé. Environ 20.000 enfants dont les parents sont ouvriers ne seront pas eux ouvriers, et celui que l’on aura choisi un peu plus haut comme possible « réfutation » faisait en réalité partie de ces 20.000.
Pour les matchs de football, c’est sensiblement pareil : pour tester la validité des modèles de prédiction, un match ne suffit pas – car il correspond à une seule observation. Il faudrait rejouer le même match, dans les mêmes conditions, des milliers de fois, et voir combien de fois il aurait été emporté par l’Angleterre, et combien de fois il aurait emporté par la Croatie. Si l’Angleterre l’avait effectivement remporté environ 666 fois, et la Croatie environ 334 fois, on aurait pu valider le modèle. Bien évidemment, une telle reproductibilité est parfaitement impossible. On retrouve là l’une des difficultés méthodologiques majeures des sciences sociales.
Une seule observation ne permet ni de valider, ni de réfuter, un modèle probabiliste. La seule attitude rigoureuse à adopter est de conclure « on ne sait pas, il faudrait des données supplémentaires pour valider ou invalider ce modèle ». Ce qui pose, me semble-t-il, une limite très forte sur ce que les modèles de prédiction d’évènements uniques et qui ne sont pas reproductibles comme les matchs de football ou les élections peuvent apporter, en tout cas si le but est d’essayer de « deviner » le résultat final. Car comment sélectionner le meilleur modèle, ou corriger celui que l’on utilise soi-même, s’il est aussi difficile de les valider, et donc de les sélectionner ?
C’est par exemple du fait de cette limite que je m’étais contenté, pendant l’élection présidentielle française de 2017, de faire une agrégation des sondages des scores des différents candidats au premier et au second tour, plutôt qu’un modèle probabiliste : ç’aurait certes été plus clinquant de dire que j’ai construit un modèle sophistiqué, avec du machine learning, des techniques statistiques novatrices, une énorme base de données, etc. Mais je reste persuadé qu’un tel modèle n’aurait pas dit grand chose de plus que la « simple » consultation des différents sondages agrégés, agrégation qui avaient le double avantage d’être à la fois plus « facile » à produire qu’un modèle prédictif[5], et plus facile à interpréter – ce qui est, me semble-t-il, un vrai enjeu tant on voit qu’interpréter correctement des probabilités est difficile.
Mon « modèle » à base de moyennes non-pondérées « prédisait » une large victoire d’Emmanuel Macron au second tour, avec un score de l’ordre de 63%. Pour celles et ceux qui connaissent le fonctionnement de la Cinquième République française, la victoire d’Emmanuel Macron ne faisait donc guère de doute. Et ce « modèle » était nettement plus facile à produire (une case à cocher dans Numbers) et à interpréter (une moyenne) qu’un modèle probabiliste.

Cela étant, ça n’est pas parce qu’il est difficile de valider les modèles prédictifs que ces derniers ne sont pas utiles. Il faut les prendre avec du recul, et notamment ne pas les sur-interpréter : une probabilité de victoire de 34% ne permet pas de dire « c’est l’Angleterre qui va gagner ». C’est plutôt une manière de traduire statistiquement le rapport de force entre les deux équipes – ou les candidats, si l’on parle d’une élection. On peut également les voir comme une manière de quantifier « l’incertitude » : plus les probabilités de victoire sont similaires, plus le résultat final sera « incertain ». Inversement, plus les probabilités sont éloignées, moins le résultat final sera « certain ».
Ces deux interprétations sont en soi déjà utiles, car elles peuvent servir à faire des commentaires mieux informés, et évitent de tomber dans le piège du bullshit que l’on entend parfois dans certains commentaires – surtout lors des élections, mais le commentaire sportif est loin d’en être immunisé…
Il faut ajouter que dans le cas spécifique du foot, c’est, au sein des sports majeurs, celui pour lequel l’aléatoire joue le plus grand rôle dans le résultat d’un match, plutôt que la différence de niveau entre les deux équipes qui s’affrontent. Et ça se comprend : il est « facile » de marquer un but, et il est possible de gagner un match en ne marquant qu’un seul but. Au basket ou au rugby, le nombre de points marqués au cours d’un match est bien plus conséquent, ce qui donne un avantage aux équipes susceptibles d’en marquer de manière répétée – donc aux « meilleures » équipes. Ce caractère aléatoire des résultats footballistiques explique certainement une partie de la popularité de ce sport, comme l’a d’ailleurs illustré cette Coupe du monde où la quasi-totalité des équipes favorites ont été rapidement éliminées.
Un dernier mot sur le modèle de Goldman Sachs : en plus d’avoir, comme les rennais et les autrichiens, calculé la probabilité des différentes équipes de gagner la compétition, les statisticiens de la banque avaient également calculé le nombre de buts probables dans différentes configurations.
On voit d’ailleurs que pour bon nombre de résultats de match prédits par ce modèle, le nombre de buts probable pour chaque équipe est proche, ce qui suggère des chances de victoire équilibrées.
À noter que la méthodologie de ce modèle n’est pas claire, mais vu les moqueries dont il fait l’objet, peut-être qu’à l’avenir il vaudra mieux éviter les modèles prédisant le nombre probable de buts, et se contenter de calculer la probabilité de gagner le match, ou éventuellement la compétition. On voit bien que la méthode des buts probables conduit à « éliminer » des équipes du modèle un peu trop rapidement, notamment lorsque l’écart de score est faible, ce qui ajoute un problème de sensibilité aux conditions initiales à des modèles dont les résultats sont déjà difficiles à interpréter par les médias et le grand public.
On pourra toutefois se rassurer en se disant que l’équipe qui a remporté la Coupe faisait partie des favoris identifiés par les trois modèles prédisant les chances de victoire, alors même qu’ils n’ont pas utilisé exactement les mêmes méthodes :
| Équipe rennaise | Équipe autrichienne | Goldman Sachs |
|---|---|---|
| Brésil : 19,1% | Brésil : 16,6% | Brésil : 18,5% |
| Allemagne : 14,5% | Allemagne : 15,8% | France : 11,3% |
| Espagne : 10,6% | Espagne : 12,5% | Allemagne : 10,7% |
| France : 9,7% | France : 12,1% | Portugal : 9,4% |
Il faut également ajouter que ces modèles ont calculé ces probabilités ex ante, c’est-à-dire avant que ne commence la compétition. Cette manière de procéder n’a pas permis de prendre en compte les matchs effectivement disputés au cours de la compétition. Il aurait certainement été intéressant de recalculer les probabilités d’emporter la compétition à mesure que les différentes équipes se sont faites éliminées. Probablement une idée à creuser pour la prochaine compétition sportive majeure !
- « The failure to accurately predict the outcome of soccer games is a good opportunity to laugh at the hubris of elite bankers, who use similar complex models for investment decisions. » ↑
- À titre de comparaison, les mêmes doctorants de l’Université de Rennes avaient estimé que pour France-Belgique, la France avait 51% de chances de l’emporter, et la Belgique le complément – 49%. On pouvait alors s’attendre à un match équilibré, qui allait basculer sur un détail ou un coup du sort. C’est sensiblement comme ça que le match s’est déroulé.En outre, le terme clé ici est « susceptible de jouer un rôle », car la probabilité ex ante de l’emporter est d’une certaine manière statistiquement « indépendante » du déroulé du match en lui-même. Je pense notamment aux faits de jeux (erreur d’arbitrage, grossière faute d’un joueur qui se fait expulser, etc.), ou si l’une des deux équipes sombre (on repense au match Brésil-Allemagne de 2014). C’est d’ailleurs pour cette raison que certains modèles prédictifs sont mis à jour au cours du match, pour refléter la probabilité de victoire compte tenu du déroulement du match. ↑
- Ils ont utilisé une méthode d’agrégation des résultats de sites de paris prédictifs en ligne, il ne s’agit pas d’une estimation basée sur des données sportives. ↑
- À titre de comparaison, FiveThirtyEight avait calculé que Donald Trump avait 29% de chances d’emporter l’élection présidentielle (https://projects.fivethirtyeight.com/2016-election-forecast/). ↑
- Je mets « facile » entre guillemets car il n’existe pas une seule méthode d’agrégation, en fait de lissage. Là aussi, j’avais opté pour une approche simple, en l’occurrence une moyenne mobile des scores par candidat pour tous les instituts de sondage, calculée sur les deux périodes précédentes. ↑
